[그래프 탐색] 플로이드 와샬
2020. 9. 20. 21:25ㆍ알고리즘/그래프 탐색
언제 쓰이는가?
- 하나의 정점에서 다른 하나의 정점까지의 최단 경로를 구하는 문제
- 하나의 정점에서 다른 모든 정점까지의 최단 경로를 구하는 문제
- 하나의 목적지로 가는 모든 최단 경로를 구하는 문제
- 모든 최단 경로를 구하는 문제
플로이드 와샬이란?
다익스트라 알고리즘과 비슷하지만
- 출발 정점이 따로 필요 없다는 점
- 음의 가중치를 가지는 간선을 쓸 수 있는 점
- 모든 정점에 대한 경로를 계산하기 때문에 거리를 저장하는 자료구조는 2차 배열이 된다.
핵심 아이디어 → '거쳐가는 정점' 을 기준으로 최단 거리를 구한다.
플로이드 와샬 알고리즘 동작 원리
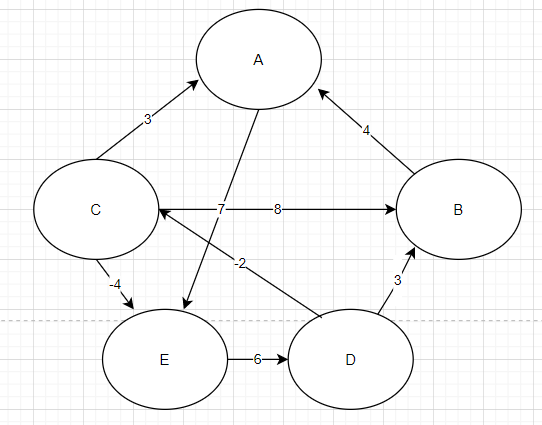
거리를 저장하는 테이블 Distance
| A | B | C | D | E | |
| A | 0 | INF | INF | INF | 7 |
| B | 4 | 0 | INF | INF | INF |
| C | 3 | 8 | 0 | INF | -4 |
| D | INF | 3 | -2 | 0 | INF |
| E | INF | INF | INF | 6 | 0 |
직전 정점을 저장한 테이블 Floyd
| A | B | C | D | E | |
| A | A | ||||
| B | B | ||||
| C | C | C | C | ||
| D | D | D | |||
| E | E |
이제 우리의 핵심 키워드 거쳐가는 정점이 'A'라 생각해보고 위의 테이블2개를 고쳐보자.
* B->A->E & C -> A -> E
이 때 거리를 저장하는 테이블에서 고려해야 할 점
Distance[B][E] = min(Distance[B][E] , Distance[B][A] + Distance[A][E])
Distance[C][E] = min(Distance[C][E] , Distance[C][A] + Distance[A][E])
거리를 저장하는 테이블 Distance
| A | B | C | D | E | |
| A | 0 | INF | INF | INF | 7 |
| B | 4 | 0 | INF | INF | 2 |
| C | 3 | 8 | 0 | INF | -4(그대로) |
| D | INF | 3 | -2 | 0 | INF |
| E | INF | INF | INF | 6 | 0 |
직전 정점을 저장한 테이블 Floyd
| A | B | C | D | E | |
| A | A | ||||
| B | B | A | |||
| C | C | C | C | ||
| D | D | D | |||
| E | E |
이렇게 쭈욱 모든 정점에 대해서 업데이트 하면 된다.
플로이드 와샬 알고리즘 구현 ( Java 코드 )
class Solution {
static int N; // 정점의 갯수
static int[][] distance = new int[N][N]; // 각 정점 들의 최단 거리
static int[][] map = new int[N][N]; // 관계
public static void floyd() {
// distance 초기값 설정
for (int i = 0; i < N; i++) {
for (int k = 0; k < N; k++) {
distance[i][k] = map[i][k] != 0 ? distance[i][k] : Integer.MAX_VALUE;
}
}
/*
* 모든 정점들을 하나씩 중간 정점에 추가한다.
* --> 반복을 시작하기 전 가장 짧은 거리가 {0,1,2, ... , k-1}
* 정점만 고려하도록 모든 정점들 쌍 사이의 거리가 가장 짧다.
* --> 반복이 끝나면 정점 번호 k가 정점 집합에 추가되고 {0,1,2,...k}가 됨.
*/
// 기준이 되는 거쳐가는 노드 K
for(int k = 1; k <= N; k++) {
// 출발하는 노드 i
for(int i=1; i <= N; i++) {
// 도착하는 노드 j
for(int j=1; j <= N; j++) {
//i에서 k를 거쳤다가 k에서 j 까지 가는 거리와 i에서 j 까지 가는 거리를 비교해서 작은 값이 최소거리이다.
distance[i][j] = Math.min(distance[i][k] + distance[k][j], distance[i][j]);
}
}
}
}
}'알고리즘 > 그래프 탐색' 카테고리의 다른 글
| [Skill] BitMask (0) | 2020.07.18 |
|---|---|
| [그래프 탐색] 다익스트라 알고리즘 (0) | 2020.06.27 |
| [그래프 탐색] 최단거리 알고리즘 종류 // 수정 예정 (0) | 2020.06.10 |
| DFS - Depth First Search (0) | 2020.06.09 |