2020. 6. 27. 01:24ㆍ알고리즘/그래프 탐색
언제 쓰이는가?
- 하나의 정점에서 다른 하나의 정점까지의 최단 경로를 구하는 문제
- 하나의 정점에서 다른 모든 정점까지의 최단 경로를 구하는 문제
- 하나의 목적지로 가는 모든 최단 경로를 구하는 문제
- 모든 최단 경로를 구하는 문제
다익스트라 알고리즘 동작 원리
다익스트라 알고리즘의 기본 로직은, 첫 정점을 기준으로 연결되어있는 정점들을 추가해가면서 최단거리를 갱신하는 것이다.
정점을 잇기 전까지는 시작점을 제외한 정점들은 모두 무한대 값을 가진다.
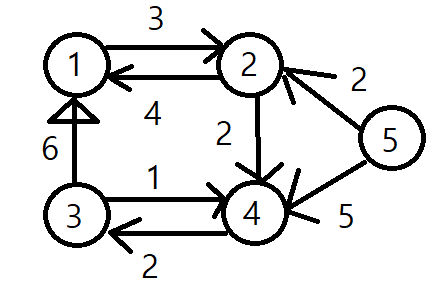
다음과 같은 그래프가 있고, 여기서 시작점은 5번의 정점이라고 생각을 해보자. 우선순위 큐에 모든 정점들을 넣어준다.
Priority Queue| 인덱스 | 최단 거리 |
| 5 | 0 |
Distance| 5 | 4 | 3 | 2 | 1 |
| 0 | INF | INF | INF | INF |
큐에서 가장 위에 있는 값을 꺼내면, 인덱스는 5이고 최소 거리가 0인 값이다.
기존에 있던 dist[5]와 큐에 있는 d와 비교를 한다. dist[5]는 d와 같기 때문에 5 주변의 인접 정점을 계산하고 기존의 dist[i]보다 더 작아지는 정점들을 큐에 넣는다.
dist[2] = min(dist[2], dist[5]+adj[5][2]) → queue add
dist[4] = min(dist[4] + dist[5] + adj[5][4]) → queue add
Priority Queue| 인덱스 | 최단 거리 |
| 2 | 2 |
| 4 | 5 |
Distance| 5 | 4 | 3 | 2 | 1 |
| 0 | 5 | INF | 2 | INF |
마찬가지로 힙에서 가장 위에 있는 값을 꺼낸다. 인덱스는 2이고 거리는 2인 값이다.
기존에 있는 dist[2]와 d를 비교한다.
dist[2] = 2이고 d는 2이기 때문에
2 주변의 인접 정점을 계산해서 기존의 dist[i]보다 더 작아지는 정점들을 큐에 넣는다.
2 주변의 인접 정점을 계산해서 기존의 dist[i]보다 더 작아지는 정점들을 큐에 넣는다.
dist[1] = min(dist[1] , d + adj[2][1] ); → queue add
dist[4] = min(dist[4] + d, + adj[2][4] ); → queue not add
Priority Queue| 인덱스 | 최단거리 |
| 1 | 4 |
| 4 | 5 |
Distance| 5 | 4 | 3 | 2 | 1 |
| 0 | 5 | INF | 2 | 4 |
마찬가지로 queue에서 가장 위에 있는 노드를 가져오면
인덱스는 1 , d는 4가 된다.
기존에 있는 dist[1] 과 d를 비교 해보면 똑같기 때문에
1 주변의 인접 정점을 계산해서 기존의 dist[i]보다 더 작아지는 정점들을 큐에 넣는다.
dist[2] = min ( dist[2], d + adj[1][2] ) → queue not add
Priority Queue| 인덱스 | 최단 거리 |
| 4 | 5 |
Distance| 5 | 4 | 3 | 2 | 1 |
| 0 | 5 | INF | 2 | 4 |
마찬가지로 queue에서 가장 위에 있는 노드를 가져오면
인덱스는 4 , d는 5가 된다.
기존에 있는 dist[4] 과 d를 비교 해보면 똑같기 때문에
4 주변의 인접 정점을 계산해서 기존의 dist[i]보다 더 작아지는 정점들을 큐에 넣는다.
dist[3] = min ( dist[3], d + adj[4][3] ) → queue add
이런식으로 쭉 해주면서 queue가 비어있을 때 까지 돌려주면 된다.
다익스트라 알고리즘 구현 ( Java 코드 )
import java.util.*;
class Solution {
public static void main(String[] args) {
}
static int N; // 정점의 갯수
static int startNode; // 출발할 정점
static int[] distance = new int[N]; // 각 정점 들의 최단 거리
static ArrayList<ArrayList<Node>> way; // 각 정점들의 관계
static PriorityQueue<Node> pq = new PriorityQueue<>(); // 우선순위 큐
public static void dijkstra(){
// distance 초기값 INF 설정.
for(int i=0; i<N; i++){
distance[i] = Integer.MAX_VALUE;
}
// 출발 정점 0으로 설정.
distance[startNode] = 0;
pq.add(new Node(startNode, 0));
while(pq.isEmpty()){
Node nowNode = pq.poll();
int nowIndex = nowNode.index, nowDistance = nowNode.distance;
if(nowDistance > distance[nowIndex]) continue;
for(int i=0; i<way.get(nowIndex).size(); i++){
int nextIndex = way.get(nowIndex).get(i).index;
int nextDistance = way.get(nowIndex).get(i).distance;
if(distance[nextIndex] > nowDistance + nextDistance){
distance[nextIndex] = nowDistance + nextDistance;
pq.add(new Node(nextIndex, distance[nextIndex]));
}
}
}
}
}
class Node implements Comparable<Node>{
int index, distance;
public Node(int index, int distance) {
this.index = index;
this.distance = distance;
}
@Override
public int compareTo(Node o) {
return distance-o.distance;
}
}'알고리즘 > 그래프 탐색' 카테고리의 다른 글
| [그래프 탐색] 플로이드 와샬 (0) | 2020.09.20 |
|---|---|
| [Skill] BitMask (0) | 2020.07.18 |
| [그래프 탐색] 최단거리 알고리즘 종류 // 수정 예정 (0) | 2020.06.10 |
| DFS - Depth First Search (0) | 2020.06.09 |